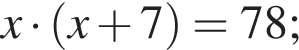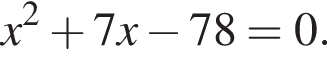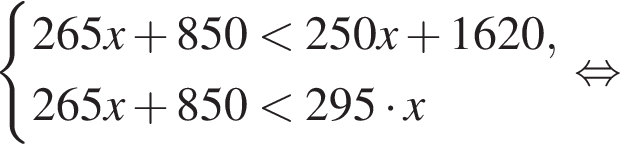Найдите площадь боковой поверхности правильной треугольной пирамиды, если длина биссектрисы ее основания равна ![]() и плоский угол при вершине
и плоский угол при вершине 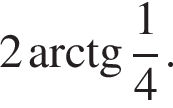
Вычислите 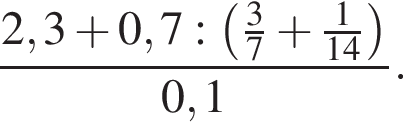
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
В основании прямой четырехугольной призмы ABCDA1B1C1D1 лежит трапеция ABCD, у которой ∠C = 90°, BC и AD — основания, BC = CC1. Плоскость, которая проходит через ребро DC и вершину A1 призмы, образует угол
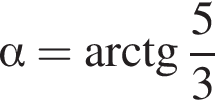 с плоскостью основания (см. рис.) и отсекает часть NC1CA1D1D. Если объем призмы равен 48, то объем оставшейся части равен … .
с плоскостью основания (см. рис.) и отсекает часть NC1CA1D1D. Если объем призмы равен 48, то объем оставшейся части равен … .
В окружность радиусом 6 вписан треугольник, длины двух сторон которого равны 6 и 10. Найдите длину высоты треугольника, проведенной к его третьей стороне.
Среди чисел 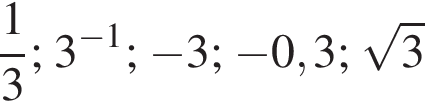 выберите число, противоположное числу 3.
выберите число, противоположное числу 3.
Площадь прямоугольника ABCD равна 50. Точки M, N, P, Q — середины его сторон. Найдите площадь четырехугольника между прямыми AN, BP, CQ, DM.
Если 16% некоторого числа равны 24, то 60% этого числа равны:
Высоты остроугольного равнобедренного треугольника ABC (AB = BC) пересекаются в точке O. Если высота AD = 16 и AO = 12, то длина стороны AC равна:
Если 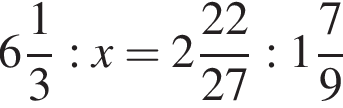 — верная пропорция, то число x равно:
— верная пропорция, то число x равно:
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 127°, ∠BOM = 153°. Найдите величину угла BOC.
Даны квадратные уравнения:
Укажите уравнение, которое не имеет корней.
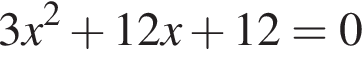
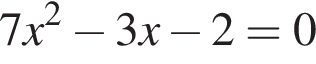
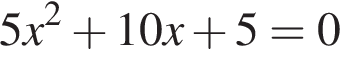
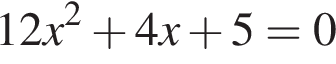
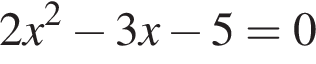
Четырехугольник MNPK, в котором ∠N = 128°, вписан в окружность. Найдите градусную меру угла K.
Решением неравенства
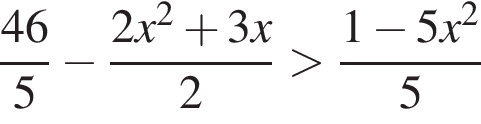
является промежуток:

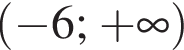
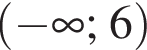
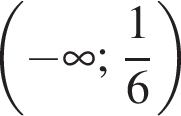
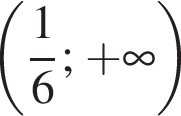
Найдите сумму целых решений неравенства 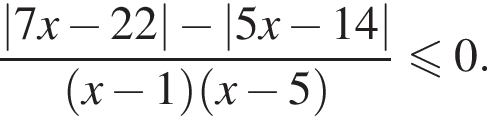
Решите неравенство 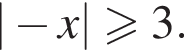
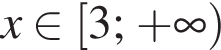

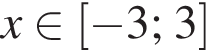
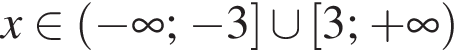
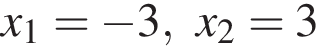
Упростите выражение 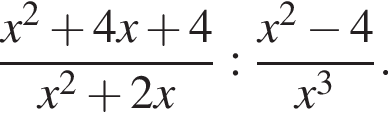
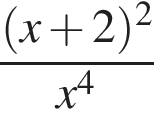
Найдите произведение корней уравнения 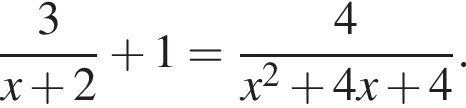
Пусть (x1; y1), (x2; y2) — решения системы уравнений 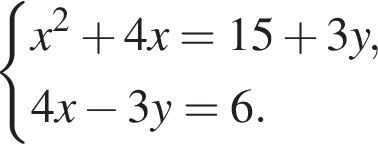
Найдите значение выражения 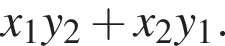
Укажите номер рисунка, на котором показано множество решений системы неравенств 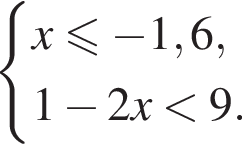
1)
2)
3)
4)
5)
Используя рисунок, определите верное утверждение и укажите его номер.


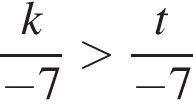
Найдите значение выражения 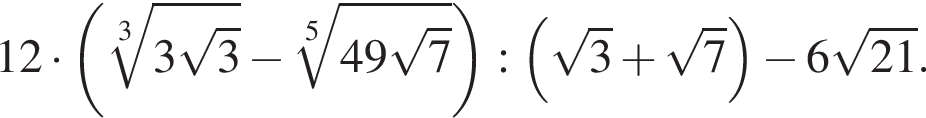
Упростите выражение 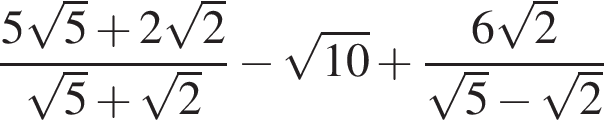
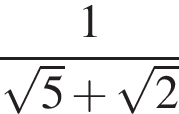
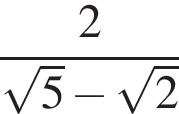
Найдите сумму корней (корень, если он единственный) уравнения 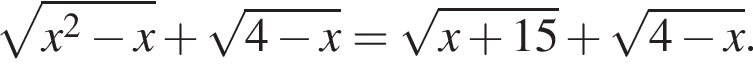
Запишите (5x)y в виде степени с основанием 5.
Найдите сумму корней уравнения 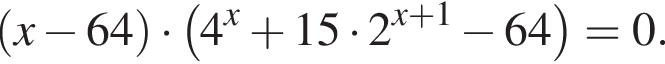
Найдите наибольшее целое решение неравенства 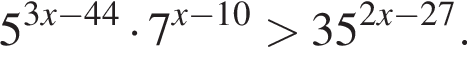
Пусть 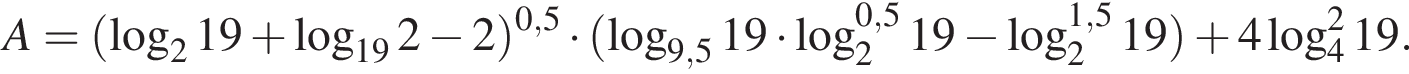
Найдите значение выражения 2A.
Корень уравнения
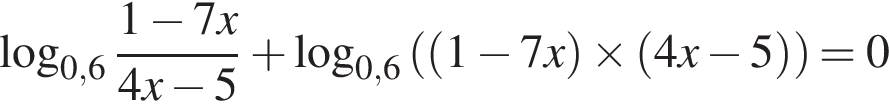
(или сумма корней, если их несколько) принадлежит промежутку:
Найдите сумму наименьшего и наибольшего целых решений неравенства 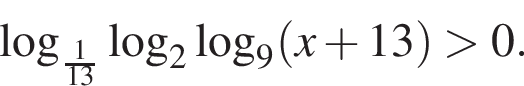
Упростите выражение 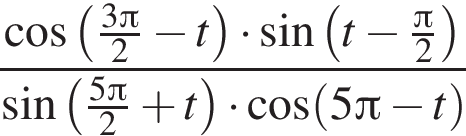
Если 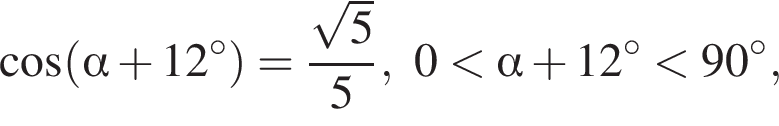 то значение выражения
то значение выражения 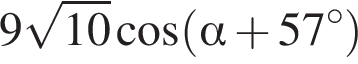 равно ...
равно ...
Найдите количество корней уравнения  на промежутке
на промежутке 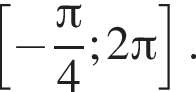
Найдите произведение корней уравнения 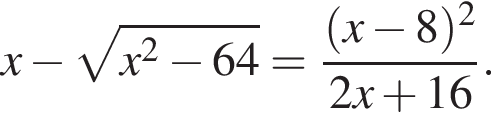
Количество целых решений неравенства 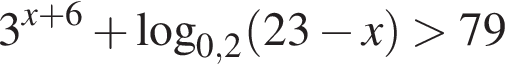 равно ...
равно ...
Запишите формулу n-го члена арифметической прогрессии (an), если даны ее первые пять членов: −10, −4, 2, 8, 14.
Найдите сумму целых значений x, принадлежащих области определения функции
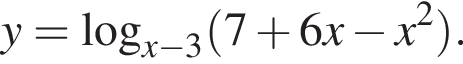
Функции заданы формулами:
1) 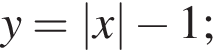 | 2) 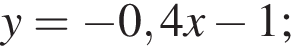 | 3) 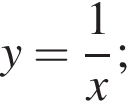 |
4) 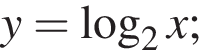 | 5) 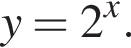 |
Выберите функцию, график которой имеет с графиком функции 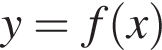 (см. рис.), заданной на промежутке [−5; 6], наибольшее количество точек пересечения.
(см. рис.), заданной на промежутке [−5; 6], наибольшее количество точек пересечения.

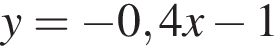
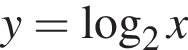
В рамках акции «Книги — детям» школа получила некоторое количество книг, распределение которых по рубрикам показано на диаграмме: «І» — учебники и учебные пособия, «ІІ» — методические пособия, «ІІІ» — научно-популярная литература, «ІV» — художественная литература (см. рис.). Какое количество учебников и учебных пособий поступило в школу, если книг научно-популярной тематики и методических пособий было 396?
На координатной плоскости изображен тупоугольный треугольник ABC с вершинами в узлах сетки (см. рис.). Косинус угла ABC этого треугольника равен:
Известно, что наименьшее значение функции, заданной формулой y = x2 + 12x + c, равно −11. Тогда значение c равно:
Из пунктов A и B, расстояние между которыми 130 км, одновременно навстречу друг другу выехали два автомобиля с постоянными и неравными скоростями: из пункта A — со скоростью a км/ч, из пункта B — со скоростью b км/ч. Через некоторое время автомобили встретились. Составьте выражение, определяющее расстояние (в километрах) от пункта B до места встречи автомобилей.
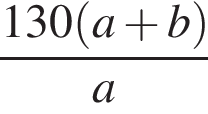
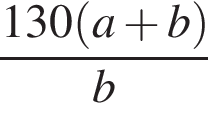
Одна из сторон прямоугольника на 7 см длиннее другой, а его площадь равна 78 см2. Уравнение, одним из корней которого является длина меньшей стороны прямоугольника, имеет вид:
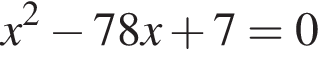 ;
;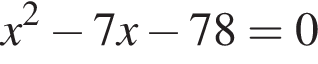 ;
;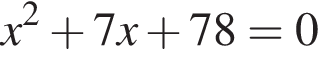 ;
;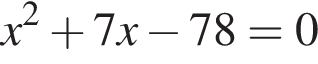 ;
;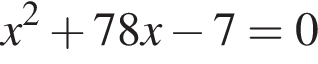 .
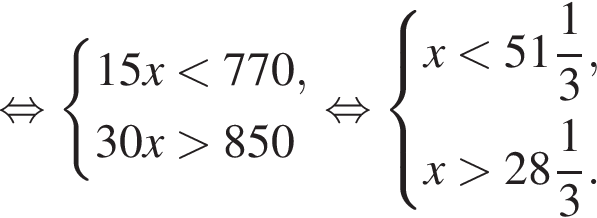
.Строительная бригада планирует заказать фундаментные блоки у одного из трех поставщиков. Стоимость блоков и их доставки указана в таблице. При покупке какого количества блоков самыми выгодными будут условия второго поставщика?
| Поставщик | Стоимость фундаментных блоков | Стоимость доставки фундаментных блоков |
|---|---|---|
| 1 | 250 | 1620 |
| 2 | 265 | 850 |
| 3 | 295 | бесплатно |
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно точки O.

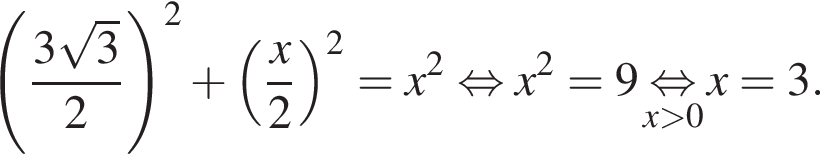
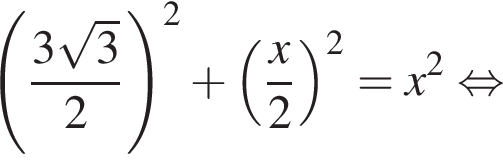
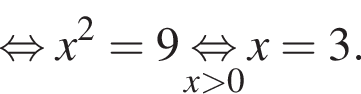
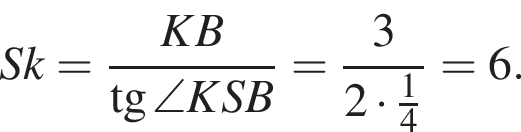
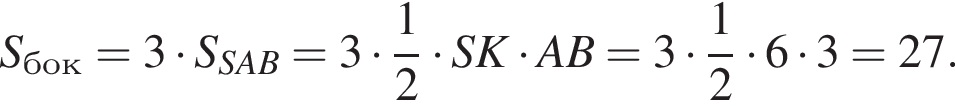
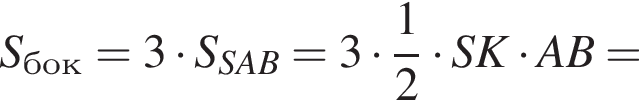
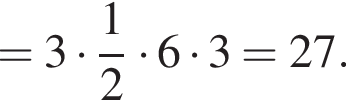
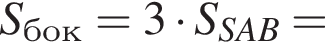
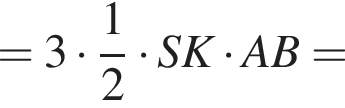
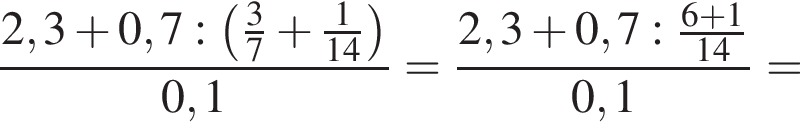
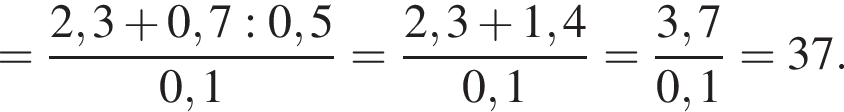
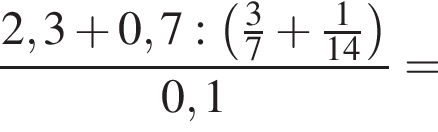
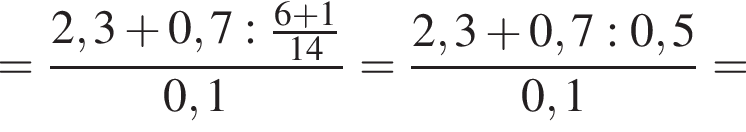
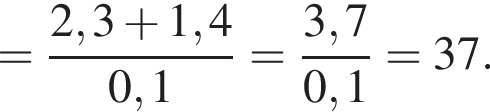
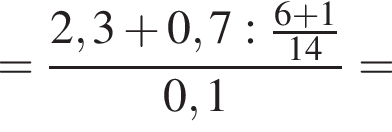
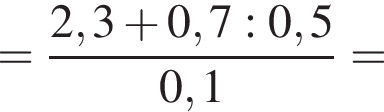
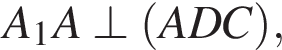
 следовательно, по теореме о трех перпендикулярах
следовательно, по теореме о трех перпендикулярах 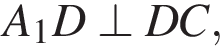 поэтому
поэтому  откуда
откуда 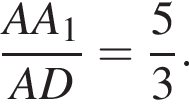 Пусть
Пусть 
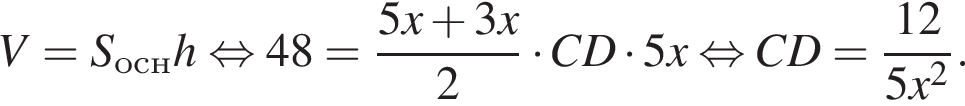
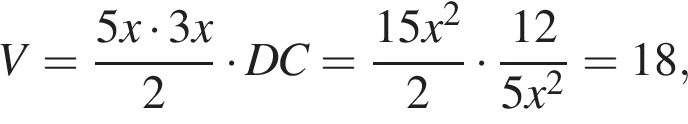 откуда
откуда 
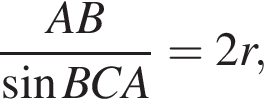 откуда
откуда 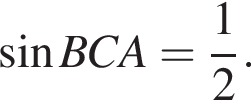 Из прямоугольного треугольника BHC имеем:
Из прямоугольного треугольника BHC имеем: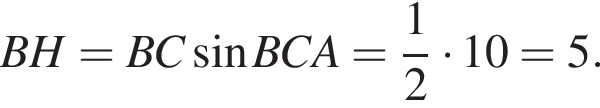
 Поскольку
Поскольку 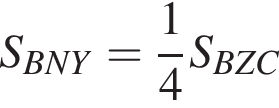 (NY — средняя линия), поэтому
(NY — средняя линия), поэтому 
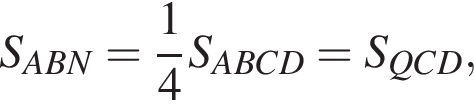 тогда
тогда 

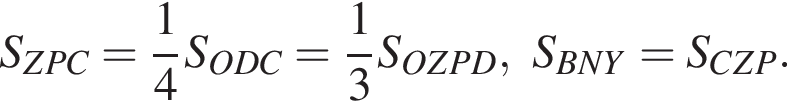
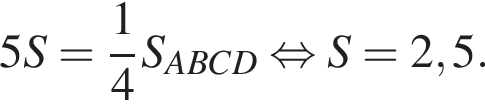
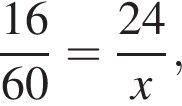 где x — неизвестное число.
где x — неизвестное число.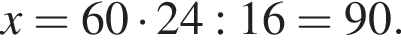
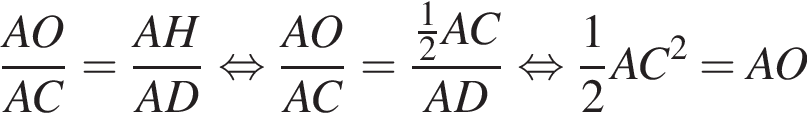
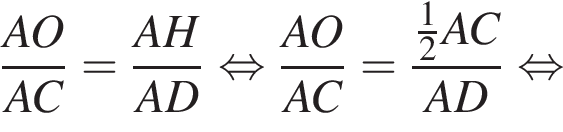
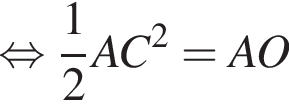

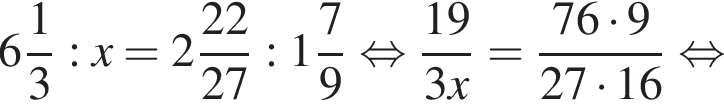
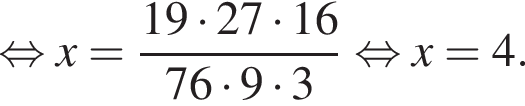
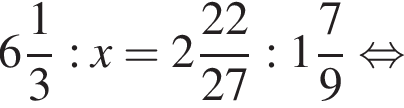
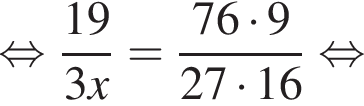
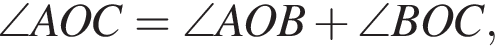
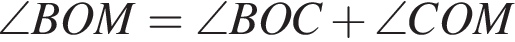 и
и  Таким образом:
Таким образом:
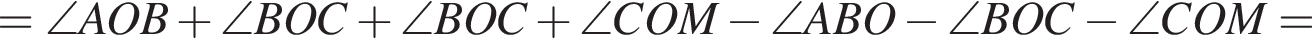
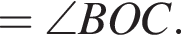

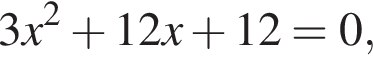 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.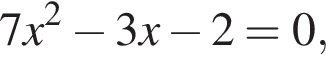 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.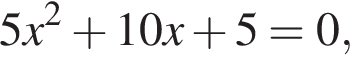 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.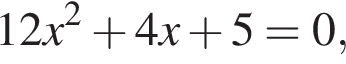 дискриминант меньше нуля, значит, корней нет.
дискриминант меньше нуля, значит, корней нет.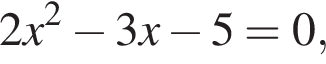 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.
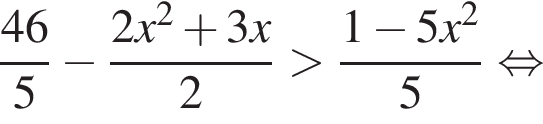
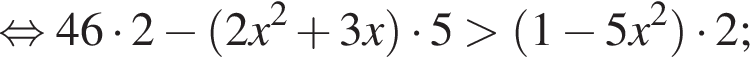
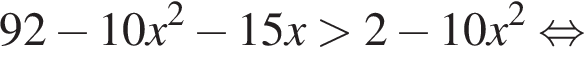

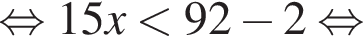

 совпадает со знаком разности
совпадает со знаком разности  имеем:
имеем: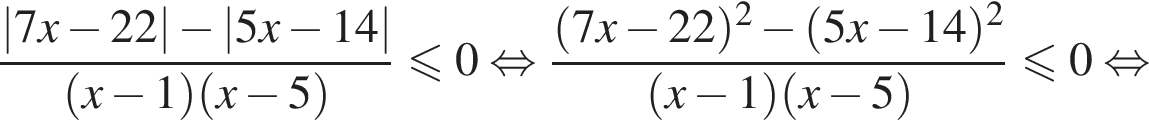
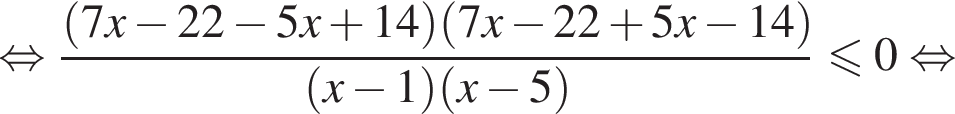
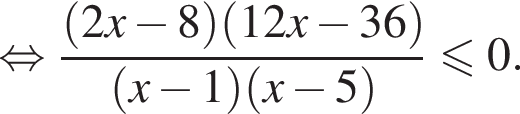
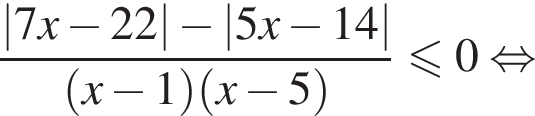
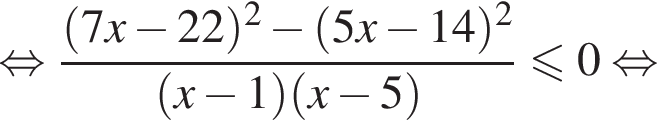
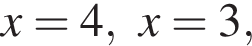 корни знаменателя
корни знаменателя 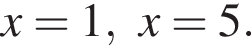 Поэтому:
Поэтому: 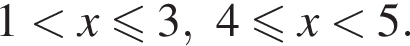 Целые решения — числа 2, 3, 4. Их сумма равна 9.
Целые решения — числа 2, 3, 4. Их сумма равна 9.
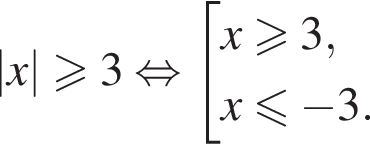
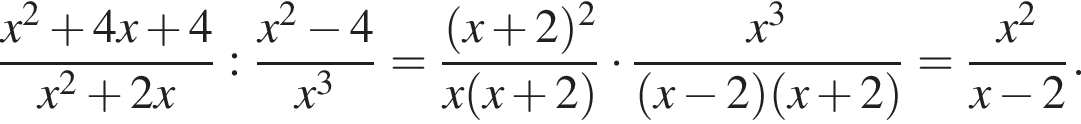
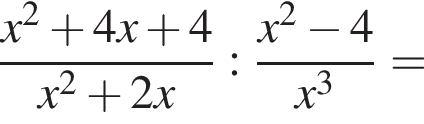
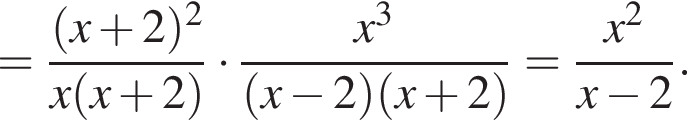
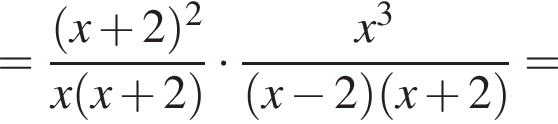
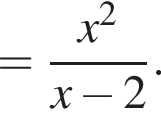
 :
: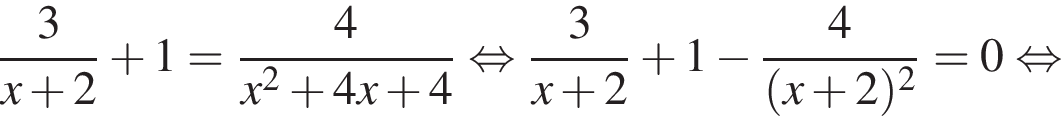
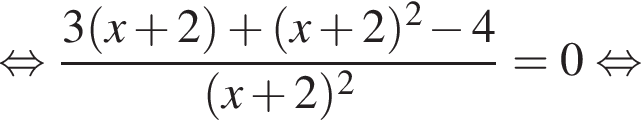

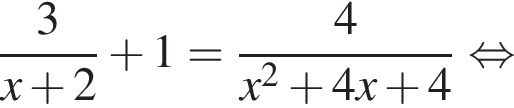
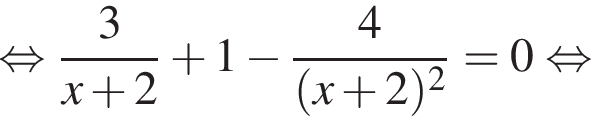
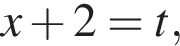 тогда:
тогда: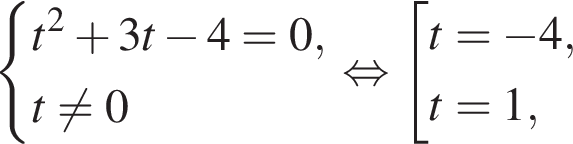
 или
или 
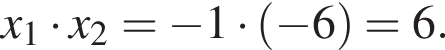
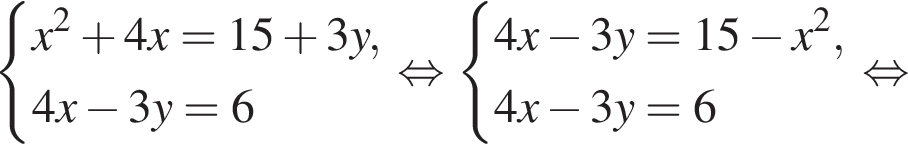
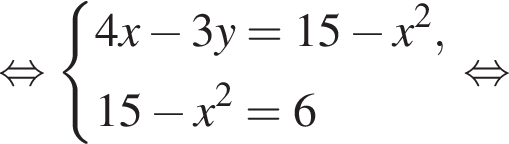
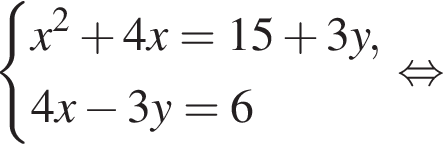
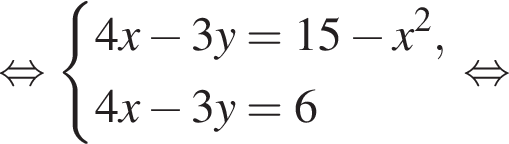
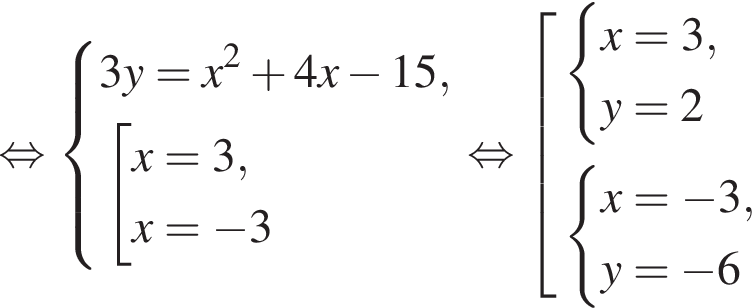

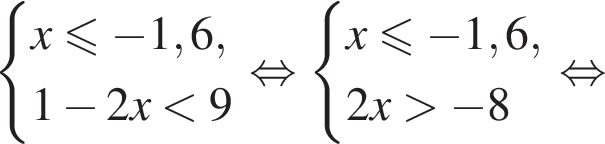
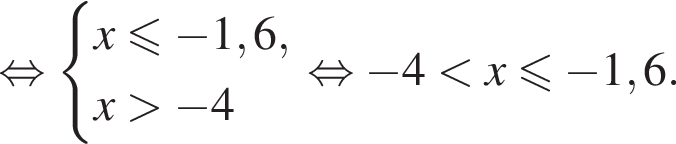
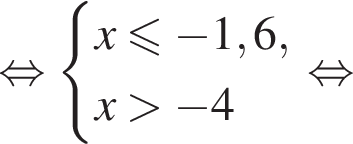
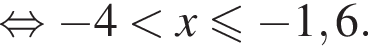
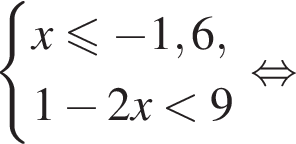
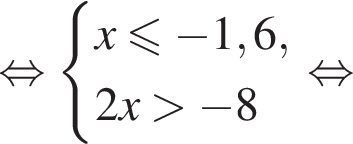
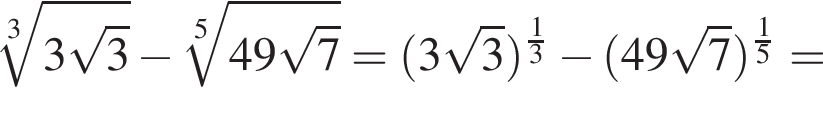
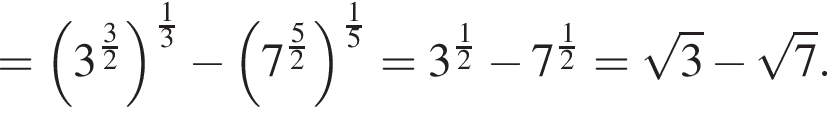
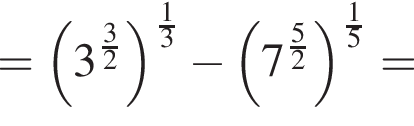
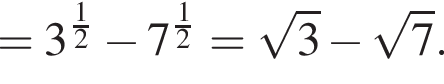
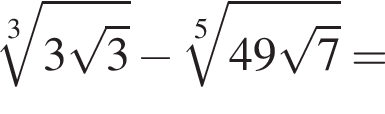
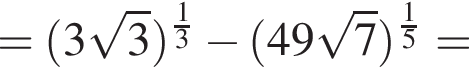
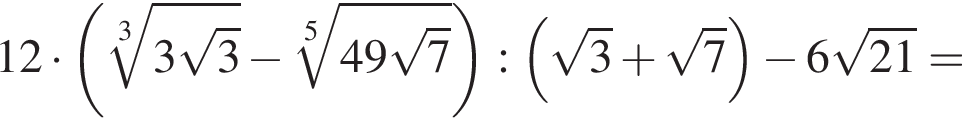
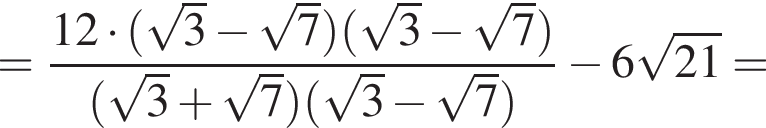
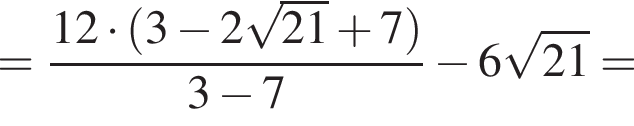
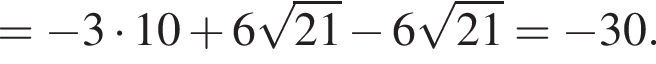

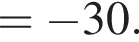
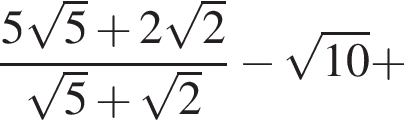
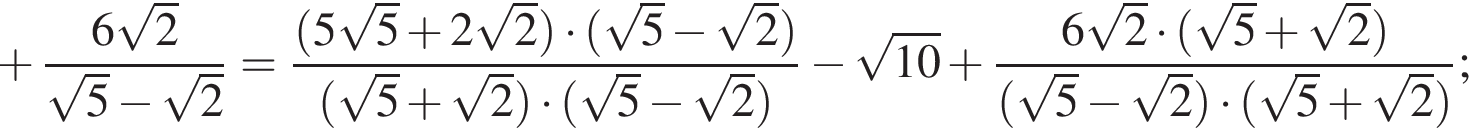
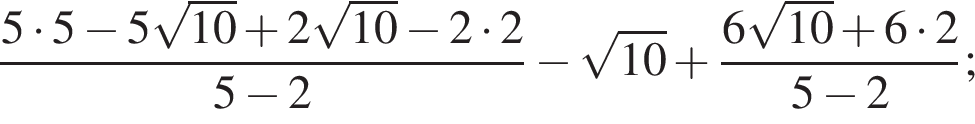
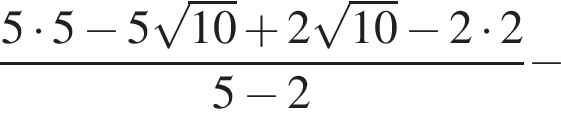
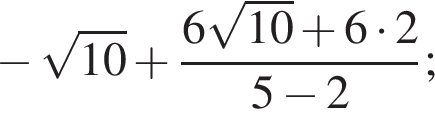
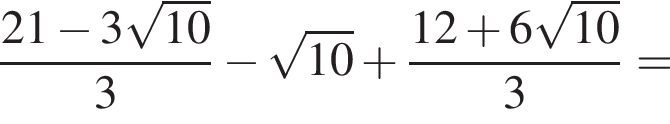
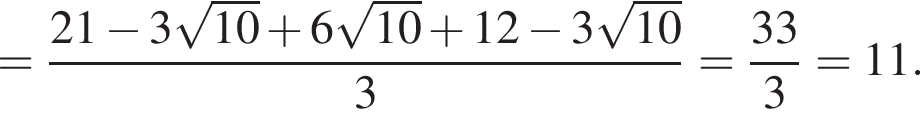
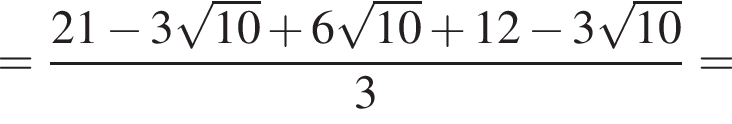
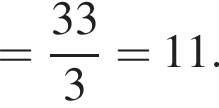
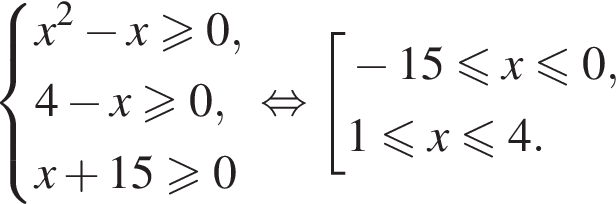
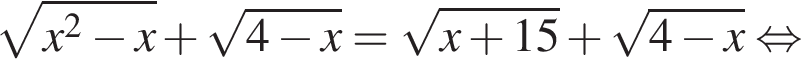
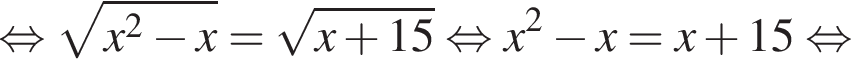
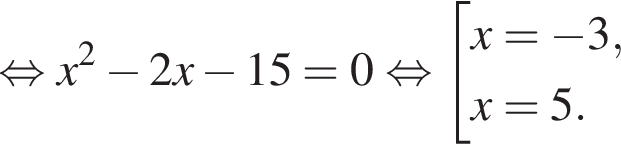
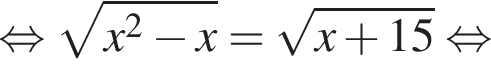

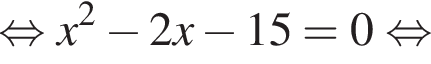
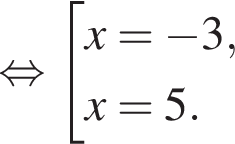

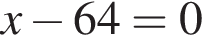 следует, что первый корень
следует, что первый корень  Рассмотрим
Рассмотрим 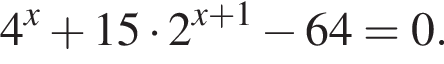 Сделаем замену
Сделаем замену 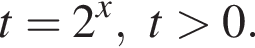 Тогда:
Тогда: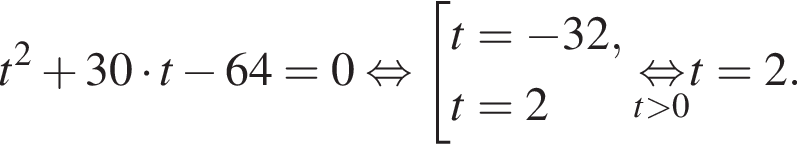
 Отсюда следует, что сумма корней уравнения равна 65.
Отсюда следует, что сумма корней уравнения равна 65.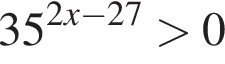 :
: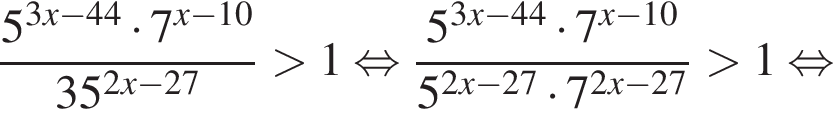
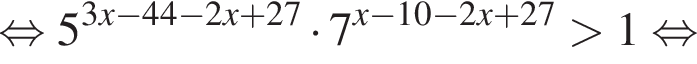
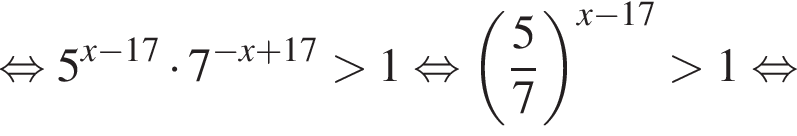
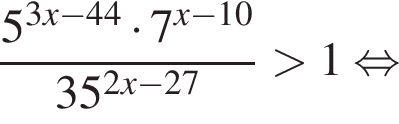
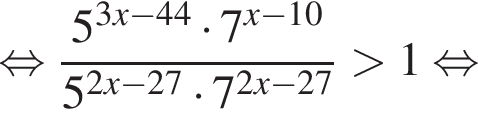
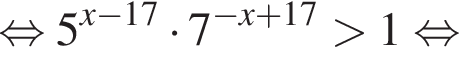
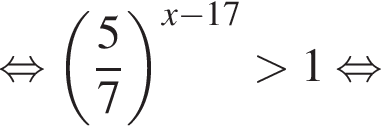
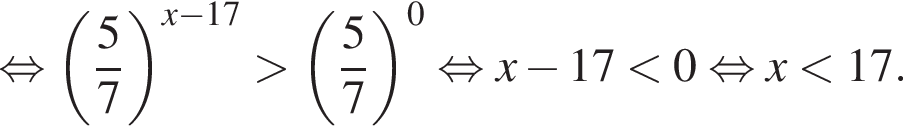
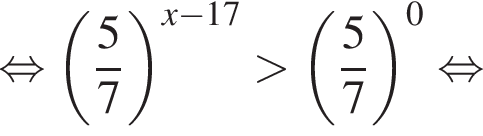
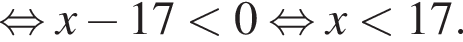
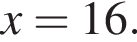
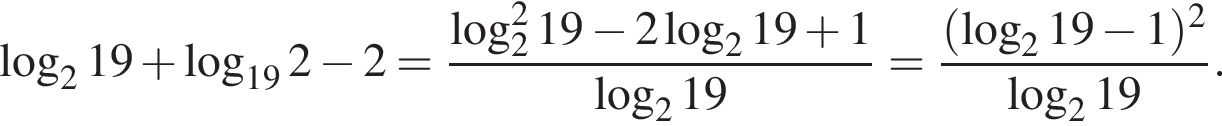
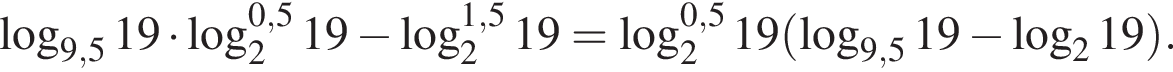
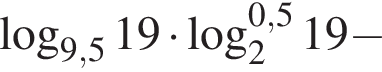
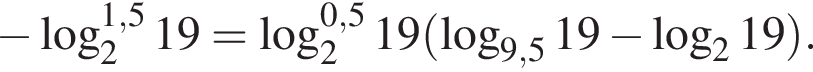
 Тогда имеем:
Тогда имеем: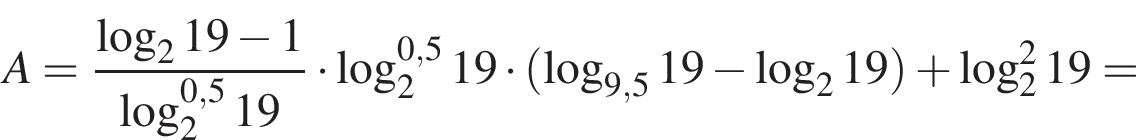
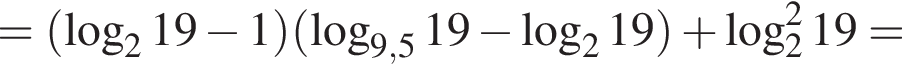
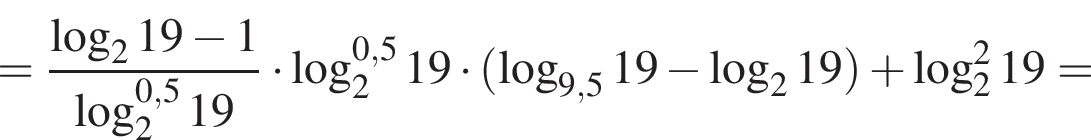
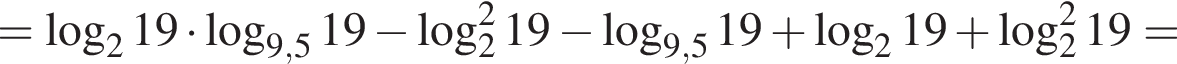
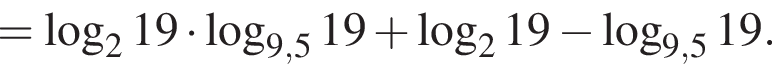
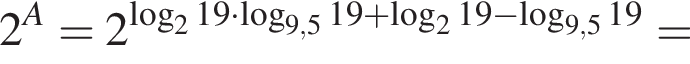
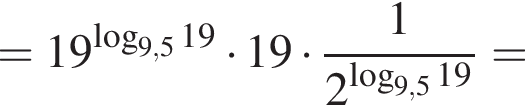
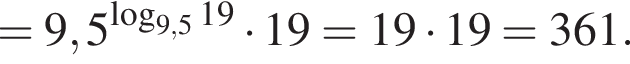
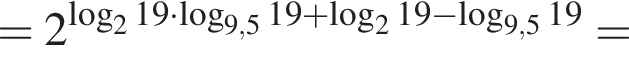
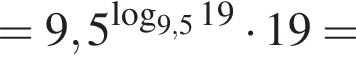
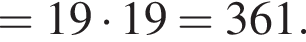
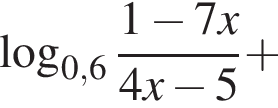
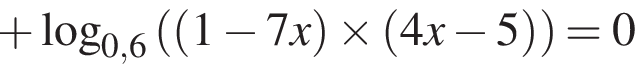
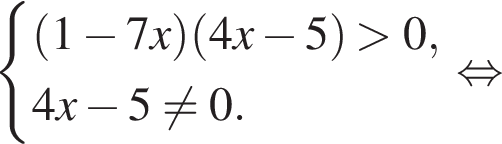
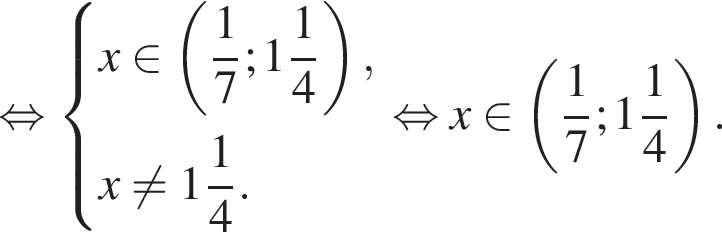
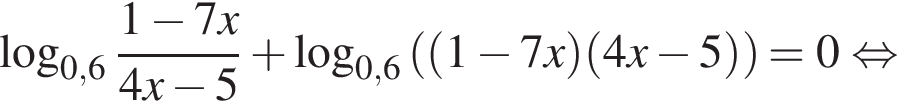
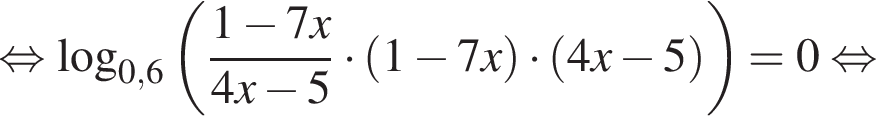
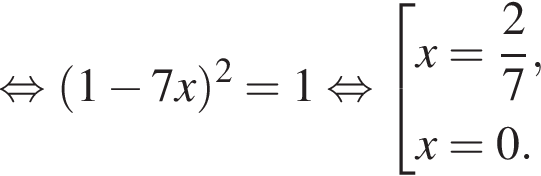
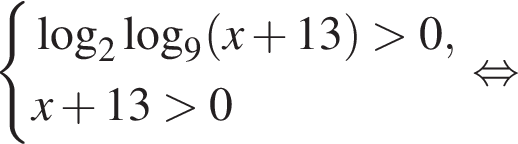
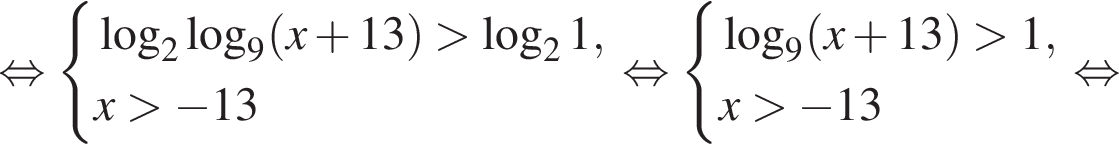
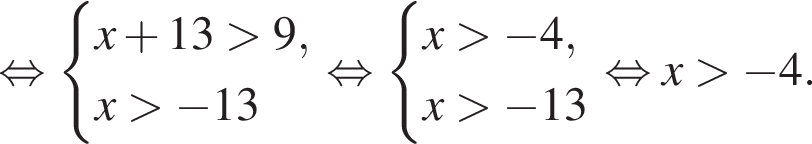
 тогда:
тогда: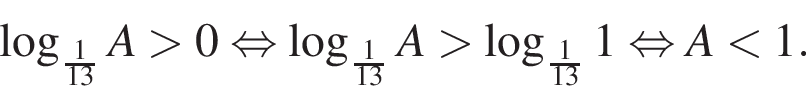
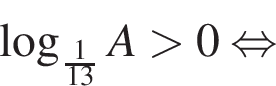
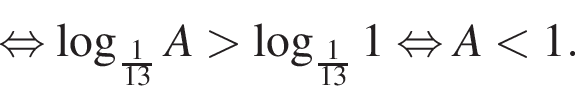

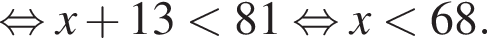

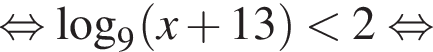
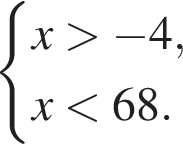 Поэтому наибольшее целое значение — 67, наименьшее целое значение −3, их сумма равна 64.
Поэтому наибольшее целое значение — 67, наименьшее целое значение −3, их сумма равна 64.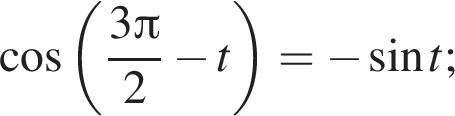
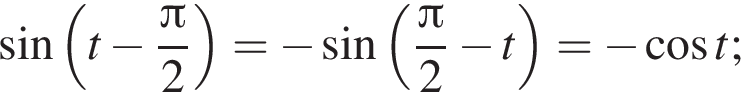
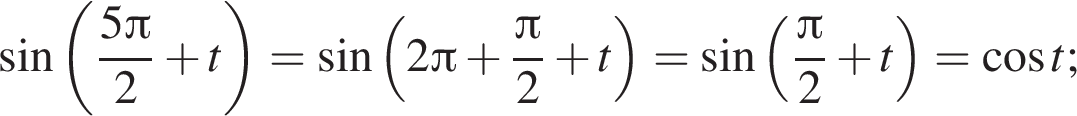
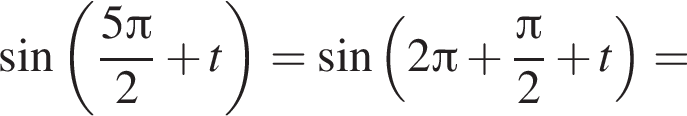
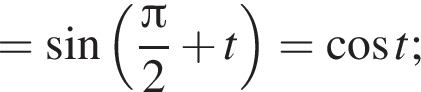
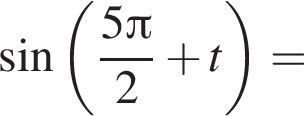
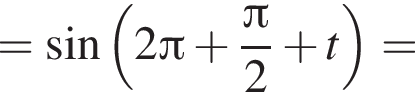
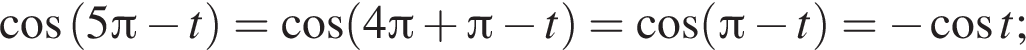

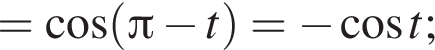
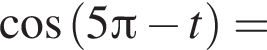
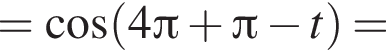
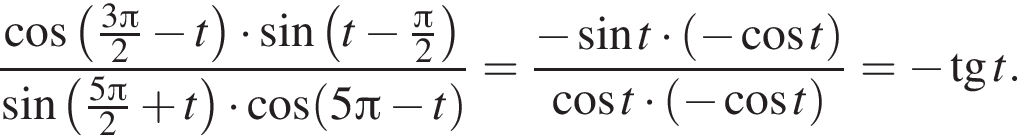
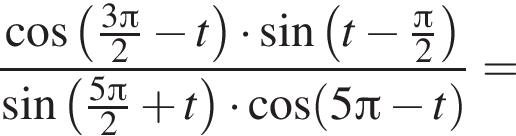
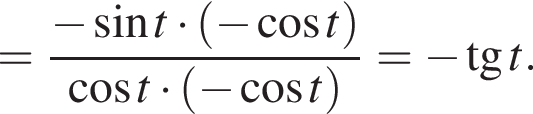
 следовательно,
следовательно, 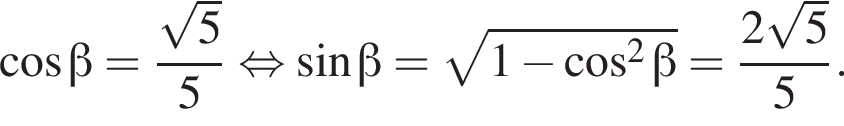
 Таким образом:
Таким образом: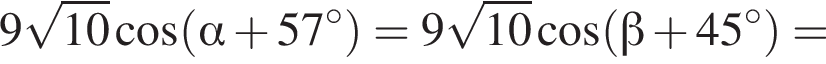
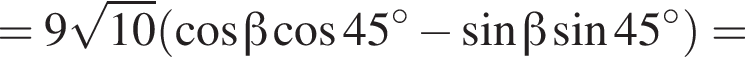
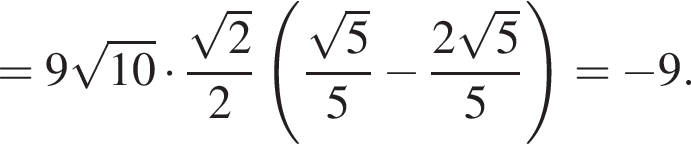
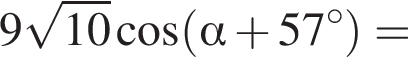
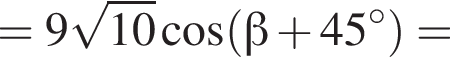
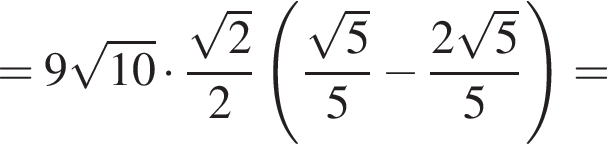

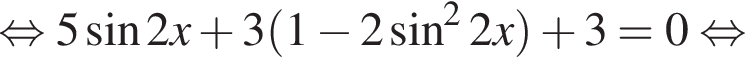
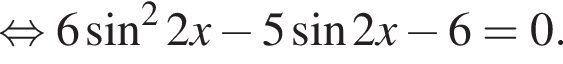
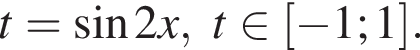 Тогда:
Тогда: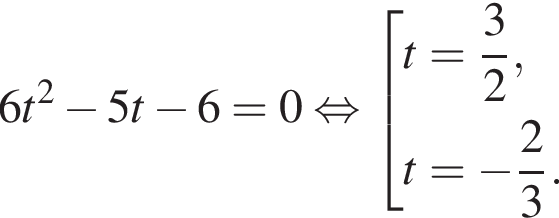
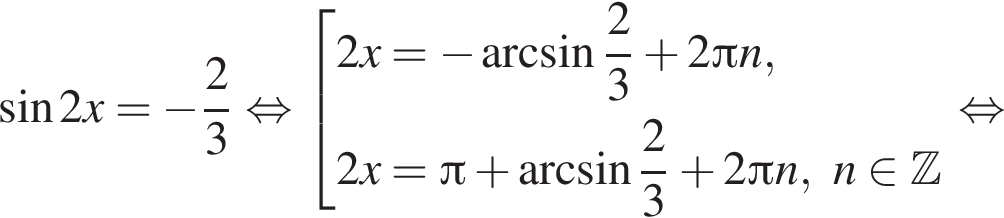
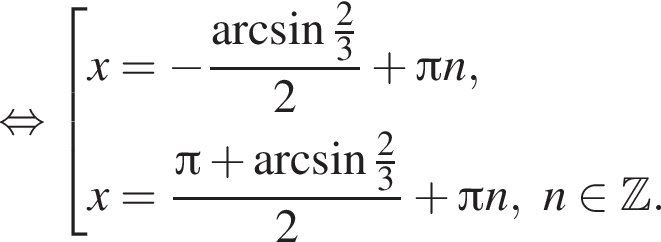
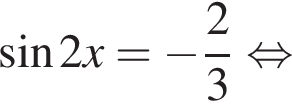
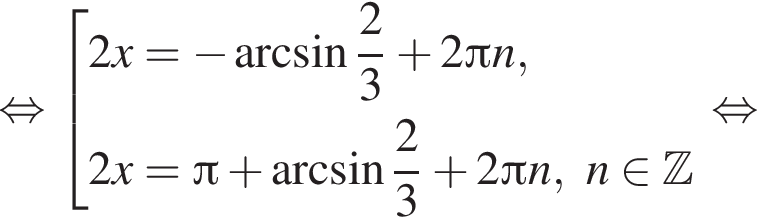
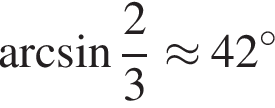 . Рассмотрим значения x при различных значениях n:
. Рассмотрим значения x при различных значениях n: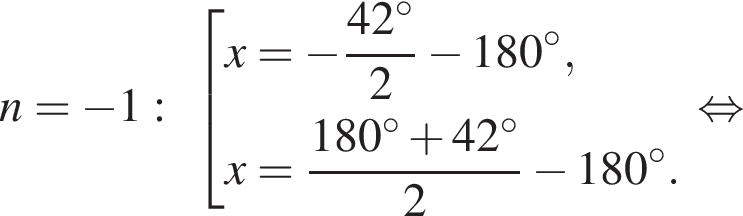
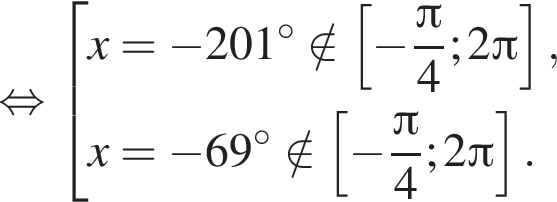
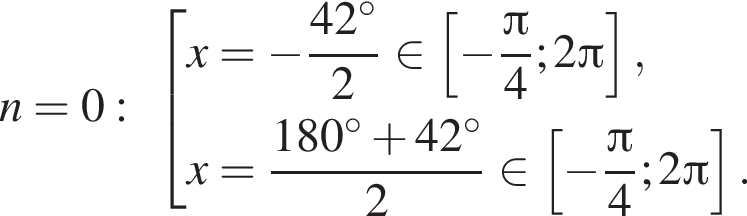
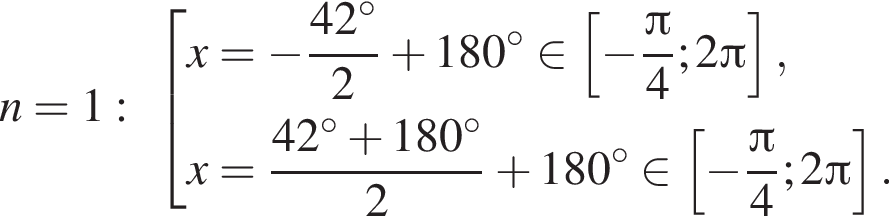
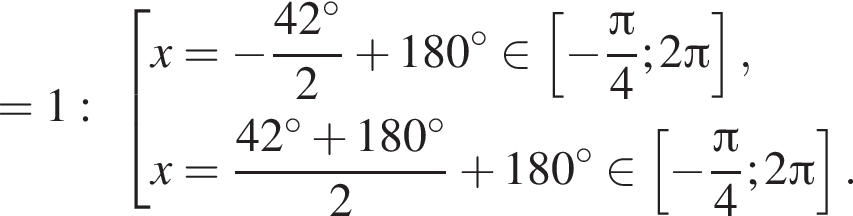
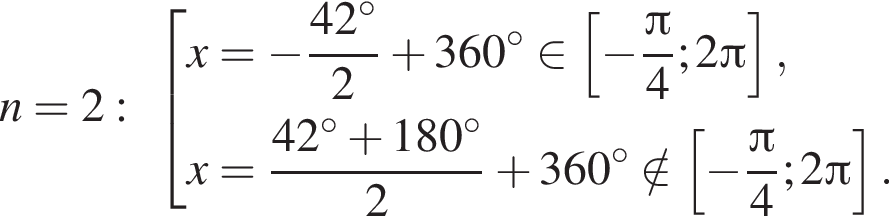
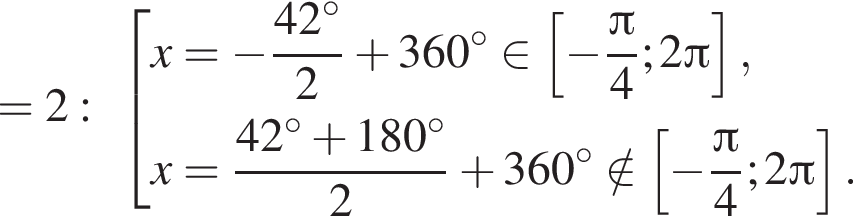
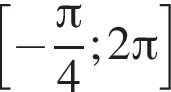 5 корней.
5 корней.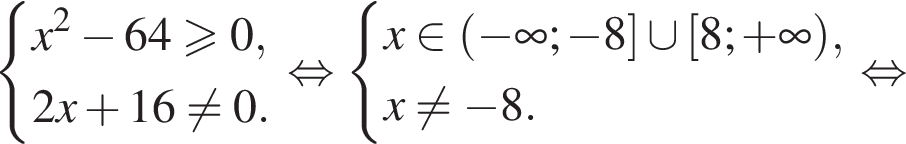
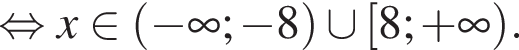
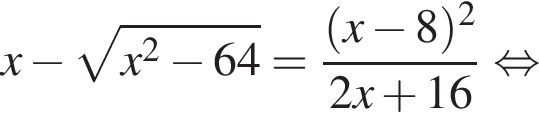
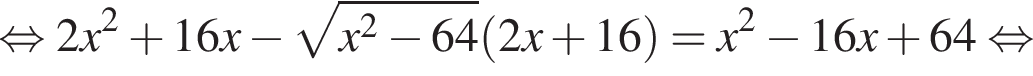
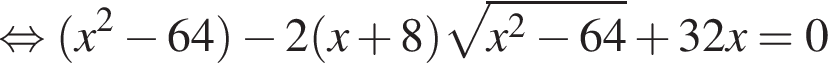
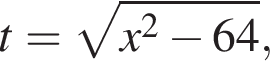 тогда
тогда 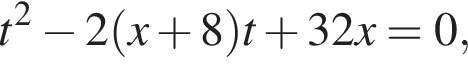 откуда
откуда 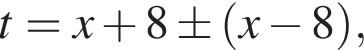 то есть
то есть 
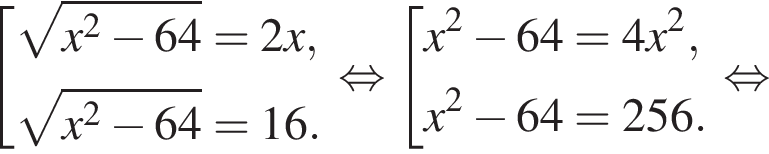

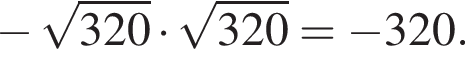
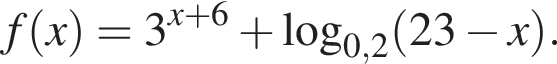 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 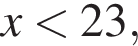 и что на
и что на 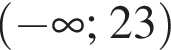
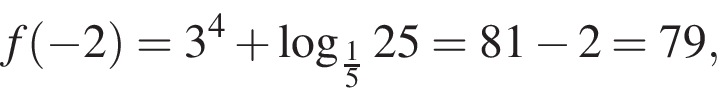 неравенство верно для всех x из
неравенство верно для всех x из 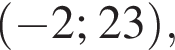 который содержит 24 целых числа.
который содержит 24 целых числа. имеем:
имеем: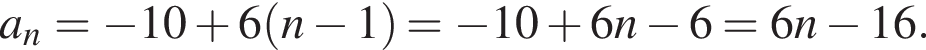
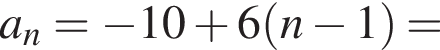

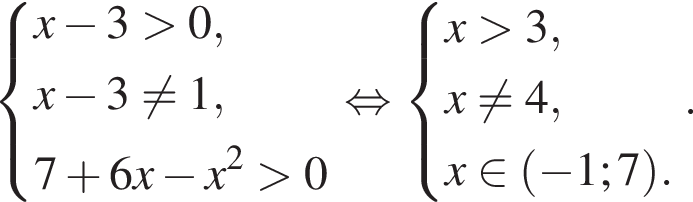
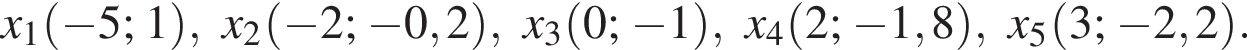

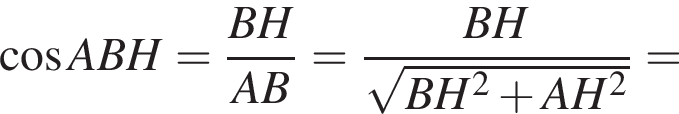
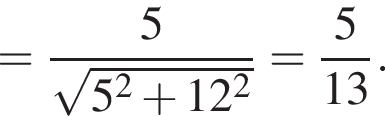
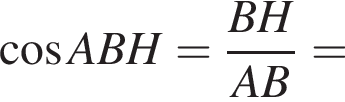
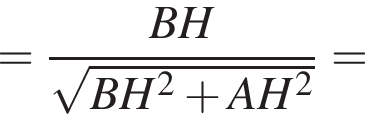
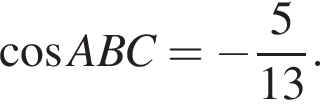
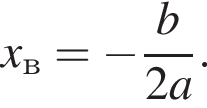 Поэтому
Поэтому 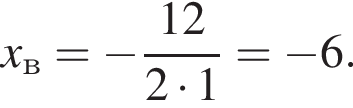 Поскольку y(xв) = −11, имеем:
Поскольку y(xв) = −11, имеем: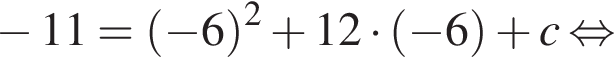


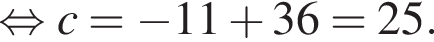
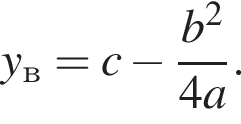
 Тогда получаем:
Тогда получаем: